Contenuto

• Passi
• Metodo 1 di 3: Parte 1: Determinazione del punto di flesso
• Metodo 2 di 3: Calcolo delle derivate di una funzione
• Metodo 3 di 3: Parte 3: Trova il punto di flesso
• Consigli

Nel calcolo differenziale, un punto di flesso è un punto su una curva in cui la sua curvatura cambia segno (da più a meno o da meno a più). Questo concetto è utilizzato in ingegneria meccanica, economia e statistica per identificare cambiamenti significativi nei dati.

Passi

Metodo 1 di 3: Parte 1: Determinazione del punto di flesso

1. 1 Definizione di funzione concava. Il centro di qualsiasi corda (un segmento che collega due punti) del grafico di una funzione concava si trova sotto il grafico o su di esso.
2. 2 Definizione di funzione convessa. Il centro di qualsiasi corda (un segmento che collega due punti) del grafico di una funzione convessa si trova sopra il grafico o su di esso.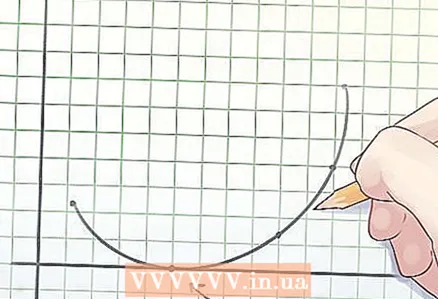
3. 3 Determinazione delle radici della funzione. La radice di una funzione è il valore della variabile "x" in cui y = 0.
   • Quando si traccia una funzione, le radici sono i punti in cui il grafico attraversa l'asse x.

Metodo 2 di 3: Calcolo delle derivate di una funzione

1. 1 Trova la derivata prima della funzione. Guarda le regole di differenziazione nel libro di testo; devi imparare a prendere le prime derivate, e solo allora passare a calcoli più complessi. Le prime derivate sono designate f '(x). Per espressioni della forma ax ^ p + bx ^ (p − 1) + cx + d, la prima derivata è: apx ^ (p − 1) + b (p - 1) x ^ (p − 2) + c.
   • Ad esempio, trova i punti di flesso della funzione f (x) = x ^ 3 + 2x -1. La derivata prima di questa funzione è:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Trova la derivata seconda della funzione. La derivata seconda è la derivata della derivata prima della funzione originale. La derivata seconda è indicata come f ′ ′ (x).
   • Nell'esempio sopra, la derivata seconda è:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Poni a zero la derivata seconda e risolvi l'equazione risultante. Il risultato sarà il punto di flesso atteso.
   • Nell'esempio sopra, il tuo calcolo è simile a questo:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Trova la derivata terza della funzione. Per verificare che il tuo risultato sia effettivamente un punto di flesso, trova la terza derivata, che è la derivata della seconda derivata della funzione originale. La terza derivata è indicata come f ′ ′ ′ (x).
   • Nell'esempio sopra, la terza derivata è:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Metodo 3 di 3: Parte 3: Trova il punto di flesso

1. 1 Controlla la derivata terza. La regola standard per stimare un punto di flesso è che se la derivata terza non è zero (cioè f ′ ′ ′ (x) ≠ 0), allora il punto di flesso è il vero punto di flesso. Controlla la terza derivata; se non è zero, hai trovato il vero punto di flesso.
   • Nell'esempio sopra, la terza derivata è 6, non 0.Quindi hai trovato il vero punto di flesso.
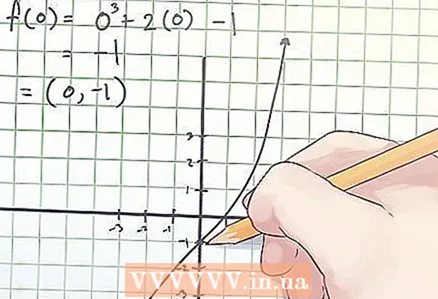2. 2 Trova le coordinate del punto di flesso. Le coordinate del punto di flesso sono indicate come (x, f (x)), dove x è il valore della variabile indipendente "x" al punto di flesso, f (x) è il valore della variabile dipendente "y" al punto di flesso punto.
   • Nell'esempio sopra, eguagliando la seconda derivata a zero, hai trovato che x = 0. Quindi, per determinare le coordinate del punto di flesso, trova f (0). Il tuo calcolo è simile a questo:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = -1.
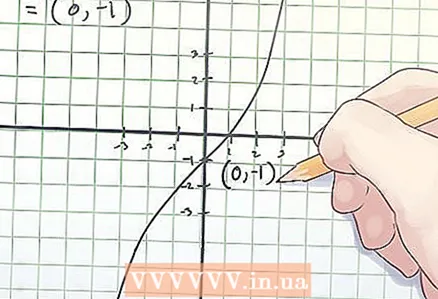3. 3 Annota le coordinate del punto di flesso. Le coordinate del punto di flesso sono i valori x e f (x) trovati.
   • Nell'esempio sopra, il punto di flesso è alle coordinate (0, -1).

Consigli

• La derivata prima di un termine libero (numero primo) è sempre zero.